Lucien, âgé de 12 ans, observe un petit morceau de mousse au microscope, découvrant la simplicité de cette structure et la beauté de sa géométrie régulière. Son professeur de sciences, ému par l’intérêt de son élève, décide de lui proposer un problème de géométrie.

• Regarde Lucien, dit-il à cet élève curieux. Tu vois la cellule centrale du végétal ? Il s’agit d’un hexagone, un polygone régulier à 6 côtés.

Figure 1

Lucien observe l’hexagone avec attention. Son professeur reprend :

• Imagine qu’on souhaite faire grandir cette figure géométrique en lui ajoutant des couronnes successives, composées de ce même hexagone. Au départ, la figure se compose d’un seul hexagone. Puis, on ajoute une première couronne, formée de 6 hexagones identiques. En tout, on obtient donc 7 hexagones.

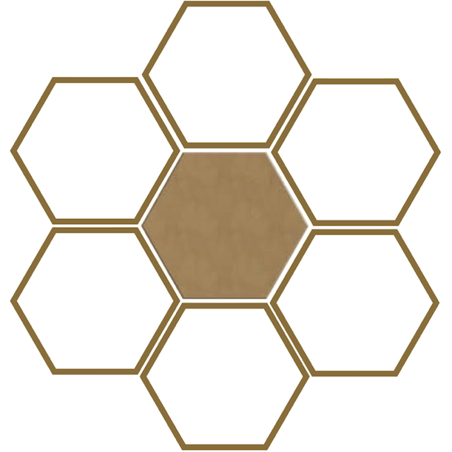
Figure 2

Lucien attrape son cahier et commence à dessiner la figure correspondant à l’étape n°1. Son professeur le félicite et poursuit : 

• À l’étape n°2, on ajoute une nouvelle couronne autour des 7 hexagones de l’étape n°1. Vas-y, complète ton dessin et dis-moi combien tu comptes d’hexagones au total.

Lucien s’exécute et répond au professeur :

• J’en compte 19.

Figure 3

• Excellent, acquiesce le professeur. À ton avis, combien d’hexagones obtiendras-tu à l’étape suivante ? Puis, à celle d’après ?
• C’est difficile à dire, répond Lucien.

Votre mission consiste à aider Lucien à répondre aux questions suivantes :

• À l’étape n°4, combien d’hexagones au total la figure comportera-t-elle ?
• À cette même étape (n°4), combien d’hexagones se situeront au bord de la figure (sur la couronne extérieure) ?
• Combien d’hexagones la figure contiendra-t-elle à l’étape n°7 ?

Indice : observez bien la suite 1 → 7 → 19 → … et la façon dont augmente le nombre d’hexagones situés au bord de la figure, à chaque nouvelle étape.